Tangential contact force in DEM

Introduction

In the previous post, we have verified the normal contact force calculations in DEM simulations. In many simple DEM codes, you will find that the inter-particle interactions only depend on the normal contact force. This is a simple enough model that can be applied to prevent large overlaps between stiff particles and to simulate the flow of particles like fluids without too much resistance. However, many behaviors of granular materials become so interesting, mysterious and hard to predict, because of the tangential or shear component of the contact force. In this post, we introduce the method to calculate the tangential contact force and present simple results to verify the model.

Model

The geometric parameters, such as the contact overlap \(\delta\) and the unit normal vector \(\boldsymbol{n}\), are defined in the same way as the normal force calculation (see the previous post). From now on, we use shear force to denote the tangential contact force as the former sounds more physical. Since the shear force depends on the relative motion at the contact point, it is convenient to first find the contact location \(\boldsymbol{x}_c\)

\[\boldsymbol{x}_c = \boldsymbol{x}_1 + (r_1 - 0.5 \delta) \boldsymbol{n}.\]

Then, the distances from the contact point to the particle centers can be calculated as

\[\delta_{c1} = |\boldsymbol{x}_c - \boldsymbol{x}_1|, \quad \delta_{c2} = |\boldsymbol{x}_c - \boldsymbol{x}_2|.\]

For simplicity, we ignore the inelastic part of the shear force. Then, its magnitude only depends on the contact deformation in the tangential direction. But how to calculate the tangential contact deformation? It is defined as the relative tangential displacement since the contact was born. This is the reason why we always say the shear force is history dependent. Mathematically, we need to track the state of every contact and do time integration. Numerically, we can accumulate the shear force step-by-step and reset it to zero once the contact disappears. So, for each time step, we first need to calculate the relative tangential velocity at the contact point

\[u_s = (\boldsymbol{u}_2 - \boldsymbol{u}_1) \cdot \boldsymbol{t} - \omega_1 \delta_{c1} - \omega_2 \delta_{c2},\]

where \(\boldsymbol{t} = (-\boldsymbol{n}[1], \boldsymbol{n}[0])\) is the unit tangential vector. The ratational velocity of particles 1 and 2 are denoted as \(\omega_1\) and \(\omega_2\), respectively. Let the anti-clockwise direction be the positive rotation. The increment of tangential displacement is

\[\Delta \delta_s = u_s \Delta t.\]

Then, we can calculate the shear force increment given the tangential contact stiffness \(k_s\)

\[\Delta \boldsymbol{F}_s = (k_s \Delta \delta_s) \boldsymbol{t}.\]

If the contact exists previously, the temporary new shear force accumulates \(\boldsymbol{F}_s \ += \Delta \boldsymbol{F}_s\), otherwise \(\boldsymbol{F}_s = \Delta \boldsymbol{F}_s\). This is only a temporary result because the shear force magnitude is also limited by the Coulomb friction \(F_f = \mu k_n \delta\). If the shear force magnitude exceeds the Coulomb friction, then

\[\boldsymbol{F}_s = \frac{F_f}{|\boldsymbol{F}_s|} \boldsymbol{F}_s.\]

The above shear force points to the tangential direction making reference to particle 1. An equal and opposite shear force (\(-\boldsymbol{F}_s\)) is applied to particle 2.

Verification

To verify the shear force calculation, we consider a simple case of two particles sliding against each other. The particle attributes are the same as the ones applied in the previous post. The two particles are initially in contact with an overlap equal to \(0.1d_p\). The friction coefficient is \(0.3\). The lower particle is again fixed. The upper particle first moves towards the right with a constant velocity of \(0.001 \ \mathrm{m/s}\) for \(0.5 \ \mathrm{s}\), and then turns around and moves with the same velocity for another \(0.5 \ \mathrm{s}\). After that, the upper particle turns around again and moves with the same velocity for another \(0.5 \ \mathrm{s}\).

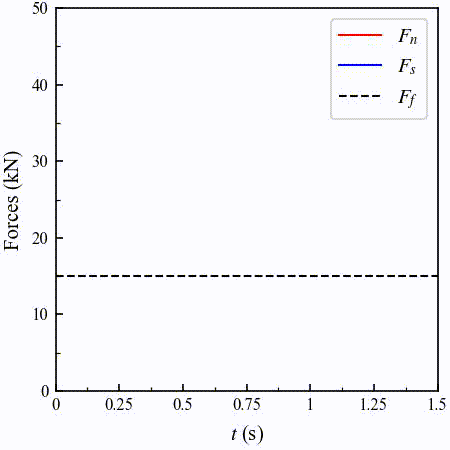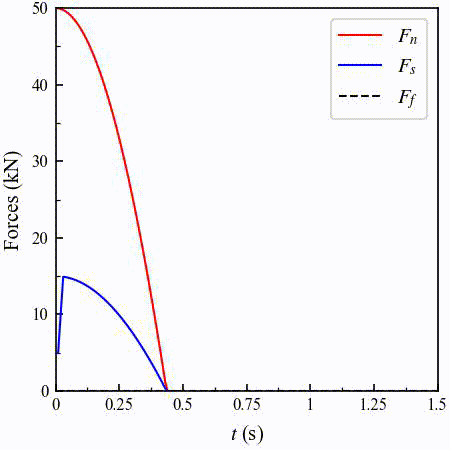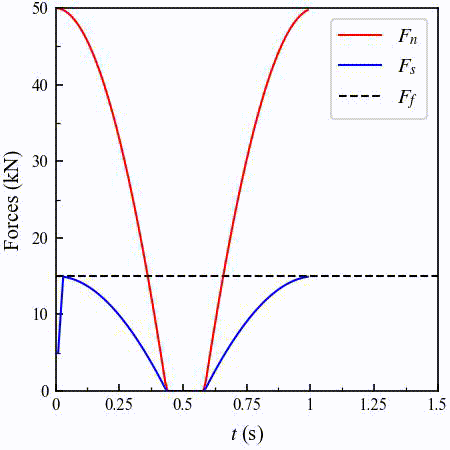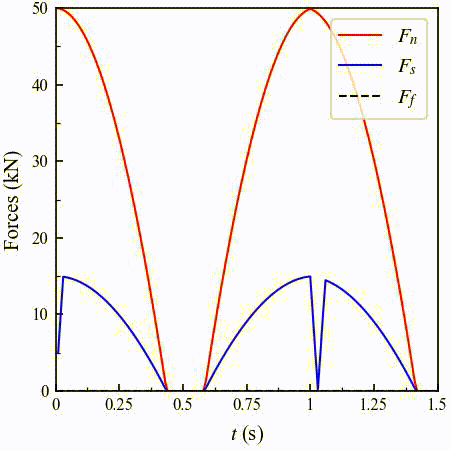
The temporal evolution of the normal force magnitude \(F_n\) is relatively easy to understand. \(F_n\) first gradually reduces as the upper particle moving towards the right because the contact overlap drops. Close to \(t=0.5 \ \mathrm{s}\), the two particles detach and the contact forces become zero. When the upper particle moves back and forth, \(F_n\) increases or decreases by following the same trend due to the constant velocity.

The temporal evolution of the shear force magnitude \(F_s\) is a bit more complex. Initially at \(t=0 \ \mathrm{s}\), the shear force is zero since there is no tangential displacement. Shortly after the upper particle moves to the right, \(F_s\) quickly increases to a value slightly less than \(30 \ \mathrm{kN}\), which is the Coulomb friction. After that, although the tangential displacement still increases, the shear force gradually decreases because of the decreasing normal force. When the upper particle moves to the left, the shear force keeps increasing but is always limited by the Coulomb friction. When the upper particle turns around again at \(t=1 \ \mathrm{s}\), the shear force quickly drops to zero and changes its direction. And then, \(F_s\) increases and gets limited by the Coulomb friction again.

To further demonstrate the significant role played by the shear force, we simulate the fall of \(8092\) particles with and without friction. The particle diameter ranges from \(4 \ \mathrm{mm}\) to \(6 \ \mathrm{mm}\). The particle density is \(100 \ \mathrm{kg/m^3}\). The contact stiffness is \(800 \ \mathrm{N/m}\). And a small restitution coefficient of \(0.001\) is applied. A small contact stiffness is adopted so that a larger time step \(10^{-4} \ \mathrm{s}\) can be used for a stable DEM simulation. Simulations with different friction coefficients, namely \(0.0\) and \(0.3\), have been conducted.

A less significent splash is observed as the friction coefficient increases. It means that the fluidity of the granular system decreases.

Summary

We have introduced the model for the calculation of tangential contact force or shear force. A simple case that involves a particle sliding over another fixed particle with some initial overlap is consider to verify the numerical calculations. Finally, we show that the shear force introduces more resistance to the granular system, thereby reducing the overall mobility.